一个椭球面以三个坐标面为对称平面,并且经过三个点（2,2,4),（0,0,6),（2,4,2),求其方程.

A.一个

B.两个

C.三个

D.四个

确定地面点经度和纬度的两个基本平面是起始子午面和（）。

A.高斯平面；

B.赤道面；

C.参考椭球面；

D.大地水准面。

证明：椭球面在其上任一点P₀(x₀，y₀，z₀)处的切平面方程为

A.具有纵向对称平面的梁发生的弯曲为平面弯曲

B.平面弯曲梁受的外力与外力偶均作用于其纵向对称平面内

C.平面弯曲梁所受的荷载可以是力，也可以是力偶

D.平面弯曲梁变形后，其轴线由直线变为荷载作用面内的平面曲线

求旋转抛物面,三个坐标平面及平面x+y=1所围有界区域的体积。

A.一个

B.都不是

C.两个

D.三个

划线时选择()平面(或线)作为划线的根据，划其他的尺寸线都从这里开始量起，这样的线或面就是划线基准。

A.一个

B.两个

C.三个

D.一个或几个

所谓半无穷范围查询(semi-infinite range query)，是教材8.4节中所介绍一般性范围查询的特例，具体地，这里的查询区域是某一侧无界的广义矩形区域，比如R=[-1，+1]x[0，﹢∞)，即是对称地包含正半y坐标轴、宽度为2的一个广义矩形区域，当然，对查询的语义功能要求依然不变——从某一相对固定的点集中，找出落在任意指定区域R内部的所有点。

范围树(176页习题[8-20])稍作调整之后，固然也可交持半无穷范围查询，但若能针对这一特定问题所固有的性质，改用优先级搜索树(priority search tree，PST)之类的数据结构，则不仅可以保持O(r+logn)的最优时间效率，而且更重要的是，可以将空间复杂度从范围树的O(nlogn)优化至O(n)。

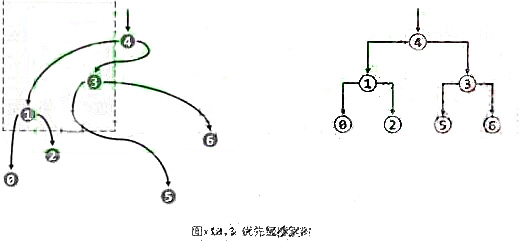
如图x10.3所示，优先级搜索树除了首先在拓扑上应是一棵二叉树，还同时遵守以下三条规则。

①首先，各节点的y坐标均不小于其左右孩子(如果存在)——因此，整体上可以视作为以y坐标为优先级的二叉堆。

②此外，相对于任一父节点，左子树中节点的x坐标均不得大于右子树中的节点。

③最后，互为兄弟的每一对左、右子树，在规模上相差不得超过一。

a)试按照以上描述，用C/C++定义并实现优先级搜索树结构;

b)试设计一个算法，在O(nlogn)时间内将平面上的n个点组织为一棵优先级搜索树;

c)试设计一个算法，利用已创建的优先级搜索树，在O(r+logn)时间内完成每次半无穷范围查询，其中r为实际命中并被报告的点数。

A.基面

B.主切削平面

C.正交平面

A.夹具找正法

B.带表中心指示器找正

C.定心显微镜找正

D.机床坐标法

E.定心轴法

F.工作台回转找正法

设碳原子的半径为r，则立方金刚石晶体中碳原子的空间占有率表达式为;

(2)在金刚石晶体中，坐标为(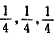)的碳原子经某一对称操作后与坐标为(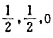)的碳原子重合则该对称操作所依据的对称元素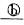为，其方位为，对称操作过程为;

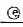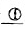(3)从某晶体中找到3个相互垂直的C₁轴(定其中一个C₂轴为主轴),2个d，则该晶体属于晶系，属于点群。

(4)某有机晶体的空间群为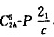，请解释该空间群记号的意义。